一倍标准差是统计学中的重要概念，揭示数据分布的离散程度和变化范围。通过计算数据的标准差，可以深入了解数据的隐藏秘密，包括异常值、数据波动和趋势变化等。一倍标准差所代表的数据变化范围，有助于分析人员更准确地把握数据的特征和规律，为决策提供依据。

本文旨在探讨一倍标准差的概念及其在数据分析中的应用，我们将介绍一倍标准差的基本定义，阐述其在统计学中的重要性，并通过实例展示如何利用一倍标准差理解数据分布、识别异常值以及进行风险管理。

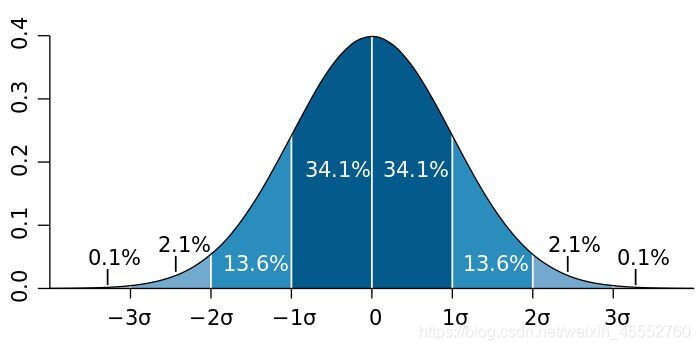
在统计学中，标准差是衡量数据集中数值离散程度的一个重要指标，它反映了数据点与平均值之间的平均距离，为我们提供了数据分布情况的直观感受，而一倍标准差，作为标准差的倍数，对于识别数据的波动范围、判断异常值以及进行数据分析具有重要意义。

一倍标准差的基本定义

一倍标准差，顾名思义，即标准差的1倍数值，在统计学中，通常将平均值加减一倍标准差的范围视为数据的合理波动区间，这是因为在这个区间内，大部分数据点都集中分布，只有少数极端值会超出这个范围。

一倍标准差在数据分析中的应用

1、理解数据分布

通过计算数据集的一倍标准差，我们可以了解数据的分布情况，如果数据集中大部分数值都集中在平均值加减一倍标准差的范围内，说明数据分布较为集中，离散程度较低，反之，如果数据点分布较为离散，则说明数据的波动性较大。

2、识别异常值

在数据分析过程中，识别异常值是非常重要的环节，通过比较数据点与平均值之间的一倍标准差距离，我们可以轻松识别出那些偏离正常范围的异常值，超过平均值加减一倍标准差范围的数据点可以被视为异常值，需要进一步检查和处理。

3、风险管理

在金融、医疗、制造等领域，风险管理是一项至关重要的任务，通过计算关键指标的一倍标准差，企业可以评估业务运营的波动性，从而制定相应的风险管理策略，在金融市场，投资者可以通过分析股票价格波动的一倍标准差来评估投资风险，并制定相应的投资策略。

实例分析

假设我们有一个关于学生考试成绩的数据集，通过对数据集的分析，我们计算出平均分为75分，标准差为10分，这意味着大部分学生的成绩都在65分至85分之间（即平均值加减一倍标准差），在这个范围内，我们可以认为数据分布较为集中，如果有学生的成绩远低于或高于这个范围，我们可以将其视为异常值，需要进一步调查原因，在教育机构或企业的质量评估中，通过分析考试成绩的一倍标准差，可以评估教学质量或业务表现的稳定性，从而制定相应的改进策略。

一倍标准差作为衡量数据离散程度的一个重要指标，在数据分析中具有广泛的应用价值，通过计算和分析一倍标准差，我们可以更好地理解数据的分布情况，识别异常值，以及进行风险管理，在实际应用中，我们应该根据具体情况灵活运用一倍标准差的概念和方法，以便更好地进行数据分析和决策支持。

展望

尽管一倍标准差在数据分析中具有重要的应用价值，但随着大数据和人工智能技术的不断发展，我们需要探索更多的数据分析方法和工具，我们可以进一步研究多倍标准差在数据分析中的应用，以及如何利用机器学习等技术提高一倍标准差计算的准确性和效率，我们还可以将一倍标准差的概念扩展到其他领域，如自然语言处理、图像识别等，为更多领域的数据分析提供有力的支持。